노이즈가 많은 데이터에서 커브를 계산

1. 회귀 스플라인: 스무딩 2입니다. 거칠기 패널티를 사용한 데이터 평활화 – 거칠기 패널티 선택 – 거칠기 패널티 행렬 자유도 매개변수 λ 3을 선택합니다. 제약 함수 – 양/음 평활화 – 단조 평활화 – 확률 밀도 함수 평활화 4입니다. 데이터에 대한 적합성 평가 [회귀 스플라인: 스무딩] 보통 regression 모델을 fit 할 때는 fit sum of squared errors (residuals)를 최소로 하는 계수를 찾는다. functional data 의 경우 회귀식은 아래 식 (1)과 같이 쓸 수 있다. $SSE\left(c\right)\ =\ \sum _j^n\left[y_j\ -\ \Phi \left(t_j\right)”c\right]^2$SSE(c) = n∑j[yj − Φ(tj)′c]2$y_j\ =\ x\left(t_j\right)\ +\ \E _j\ =\ \Phi “\left(t_j\right)c\ +\ \E _j\ \ \ \ \ \left(1\right)$yj = x(tj) + ℇj = Φ′(tj)c + ℇj (1)$\Rightarrow \ y\ =\ \Phi c\ +\ \E ,\ \hat{c}\ =\ \left(\Phi “\Phi \right)^{-1}\Phi “y$⇒ y = Φc + ℇ, ^ c= (φ’φ) -1 φ’y 입니다 1. 회귀 스플라인: 스무딩 2입니다. 거칠기 패널티를 사용한 데이터 평활화 – 거칠기 패널티 선택 – 거칠기 패널티 행렬 자유도 매개변수 λ 3을 선택합니다. 제약 함수 – 양/음 평활화 – 단조 평활화 – 확률 밀도 함수 평활화 4입니다. 데이터에 대한 적합성 평가 [회귀 스플라인: 스무딩] 보통 regression 모델을 fit 할 때는 fit sum of squared errors (residuals)를 최소로 하는 계수를 찾는다. functional data 의 경우 회귀식은 아래 식 (1)과 같이 쓸 수 있다. $SSE\left(c\right)\ =\ \sum _j^n\left[y_j\ -\ \Phi \left(t_j\right)”c\right]^2$SSE(c) = n∑j[yj − Φ(tj)′c]2$y_j\ =\ x\left(t_j\right)\ +\ \E _j\ =\ \Phi “\left(t_j\right)c\ +\ \E _j\ \ \ \ \ \left(1\right)$yj = x(tj) + ℇj = Φ′(tj)c + ℇj (1)$\Rightarrow \ y\ =\ \Phi c\ +\ \E ,\ \hat{c}\ =\ \left(\Phi “\Phi \right)^{-1}\Phi “y$⇒ y = Φc + ℇ, ^ c= (φ’φ) -1 φ’y 입니다

data (” growth”, package=’fda’) age <-growth$age height basis12 <-create.bspline.basis(c(1,18), 12, 6) basismat <-growth$hgtm height coff <-lsfit(basismat, heightmat, intercept) <-eval.basis(age, height basismat) height coff <-lsmat <-growthmat, intercept>=FALSE)$coffheightList <- smooth.basis(年齢、身長の基準 12) # 위 과정을 쉽게 하는법 heightfd <- heightList$fdfd$coffheight.df <- heightList$dfheight.gcv <- heightList$gcv y2cMap <- solve(crossrod(basismat)), t(basismat)y2cfatmat <- he> y2cmatmat %mat %* マップ <- he> data (” growth”, package=’fda’) age <-growth$age height basis12 <-create.bspline.basis(c(1,18), 12, 6) basismat <-growth$hgtm height coff <-lsfit(basismat, heightmat, intercept) <-eval.basis(age, height basismat) height coff <-lsmat <-growthmat, intercept>=FALSE)$coffheightList <- smooth.basis(年齢、身長の基準 12) # 위 과정을 쉽게 하는법 heightfd <- heightList$fdfd$coffheight.df <- heightList$dfheight.gcv <- heightList$gcv y2cMap <- solve(crossrod(basismat)), t(basismat)y2cfatmat <- he> y2cmatmat %mat %* マップ <- he>

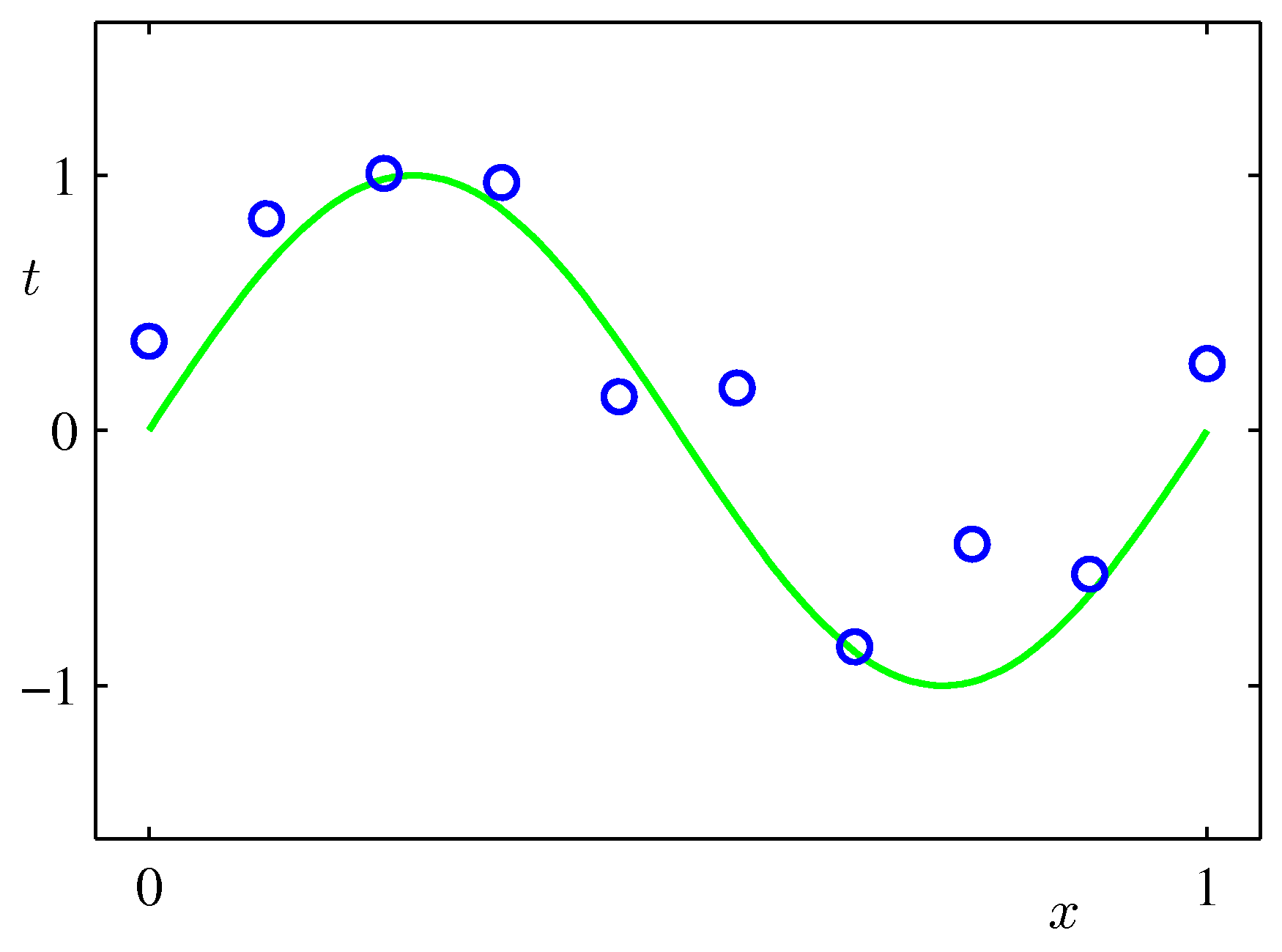
위의 코드는 regression smoothing을 하는 순서입니다. 여기서는 growth라는 데이터 세트를 사용했는데, 이 데이터 세트는 1세부터 18세까지의 39명의 소년과 54명의 소녀들의 키 데이터를 가지고 있습니다. 지금 목표는 age를 설명변수로, 키를 반응변수로 설정하고 regression을 적합시키는 것입니다. R에서는 이미 함수로 저장되어 있기 때문에 쉽게 진행할 수 있습니다. lsfit() 함수에 age로 평가된 basis matrix와 height matrix를 넣는 것입니다. age 범위를 range로 하고 basis function의 수는 12개로 설정한 bspline basis function을 만든 후 basis matrix를 만들 수 있고 growth 데이터셋의 남자아이 키데이터를 heightmatrix로 지정하였습니다. 그리고 coefficeints만 뽑아내면 heightcoef에 regression으로 적합한 계수가 저장됩니다. 상기 과정은 smooth 입니다. basis() 함수로 더 쉽게 할 수 있습니다. 함수안 인자로 설명변수, 반응변수, basis function을 입력하면 한 줄로 피팅이 끝나버립니다. fit된 curve를 fd class로 따로 빼낼 수도 있고, curve의 degree of freedom이나 generalized cross-validation value를 빼낼 수도 있습니다. 위에서 hieghtcoef, heightfd$coefs와 같은 coefficients를 누군가가 이미 만들어놓은 함수로 계산을 했는데 굳이 라이브러리를 사용하지 않더라도 설명변수로 평가된 basisfunction만 있으면 쉽게 c-hat 값을 추정할 수 있습니다. 위 식 (1)에서 least-squares 방식으로 c-hat을 추정한 식을 이용하면 y2cMap((X’X’X)-1X’)을 계산할 수 있으며 이 값을 반응변수 matrix와 곱하면 끝입니다. 또한 X(X’X)-1X’로 정의되는 hat matrix도 마찬가지로 쉽게 구할 수 있으며, hat matrix와 반응변수 matrix의 곱으로 y-hat을 추정할 수도 있습니다. y-hat 값을 보면 남자아이는 나이가 들수록 키가 커지는 형태를 보이며, 특히 공통적으로 5번째 index(2세)부터 10번째 index 부근(7세)까지 급격한 성장을 이룬다는 점을 알 수 있습니다. 위의 코드는 regression smoothing을 하는 순서입니다. 여기서는 growth라는 데이터 세트를 사용했는데, 이 데이터 세트는 1세부터 18세까지의 39명의 소년과 54명의 소녀들의 키 데이터를 가지고 있습니다. 지금 목표는 age를 설명변수로, 키를 반응변수로 설정하고 regression을 적합시키는 것입니다. R에서는 이미 함수로 저장되어 있기 때문에 쉽게 진행할 수 있습니다. lsfit() 함수에 age로 평가된 basis matrix와 height matrix를 넣는 것입니다. age 범위를 range로 하고 basis function의 수는 12개로 설정한 bspline basis function을 만든 후 basis matrix를 만들 수 있고 growth 데이터셋의 남자아이 키데이터를 heightmatrix로 지정하였습니다. 그리고 coefficeints만 뽑아내면 heightcoef에 regression으로 적합한 계수가 저장됩니다. 상기 과정은 smooth 입니다. basis() 함수로 더 쉽게 할 수 있습니다. 함수안 인자로 설명변수, 반응변수, basis function을 입력하면 한 줄로 피팅이 끝나버립니다. fit된 curve를 fd class로 따로 빼낼 수도 있고, curve의 degree of freedom이나 generalized cross-validation value를 빼낼 수도 있습니다. 위에서 hieghtcoef, heightfd$coefs와 같은 coefficients를 누군가가 이미 만들어놓은 함수로 계산을 했는데 굳이 라이브러리를 사용하지 않더라도 설명변수로 평가된 basisfunction만 있으면 쉽게 c-hat 값을 추정할 수 있습니다. 위 식 (1)에서 least-squares 방식으로 c-hat을 추정한 식을 이용하면 y2cMap((X’X’X)-1X’)을 계산할 수 있으며 이 값을 반응변수 matrix와 곱하면 끝입니다. 또한 X(X’X)-1X’로 정의되는 hat matrix도 마찬가지로 쉽게 구할 수 있으며, hat matrix와 반응변수 matrix의 곱으로 y-hat을 추정할 수도 있습니다. y-hat 값을 보면 남자아이는 나이가 들수록 키가 커지는 형태를 보이며, 특히 공통적으로 5번째 index(2세)부터 10번째 index 부근(7세)까지 급격한 성장을 이룬다는 점을 알 수 있습니다.

yhat <-햇 매트 %*% 높이 매트 플롯(yhat, 유형= ‘b’, pch=19, lty=1, xlab= ‘연령 지수’, ylab= ‘높이’) yhat <-햇 매트 %*% 높이 매트 플롯(yhat, 유형= ‘b’, pch=19, lty=1, xlab= ‘연령 지수’, ylab= ‘높이’)

 

단, 이러한 regression approach는 basis function의 수(여기서는 12)가 sampling points n보다 훨씬 작은 경우에만 적합할 수 있다는 제약조건이 있다. 베이시스 기능 수가 크면 데이터를 과소평가하거나 과대평가할 가능성이 커지기 때문이다. 또, regression splines의 미분 추정치는 다소 불안정한 경향이 있다. 이에 smoothing의 제약조건이 조금 완화된 형태로 미분 추정치도 보다 정확하게 만들어내는 접근법이 연구됐다. [Data Smoothing with Roughness Penalties] roughness penalty 어프로치는 basis function의 수를 대폭 늘리는 것이다. 예를 들면, 상기의 growth 데이터는 아이 1명당 31개의 관측치가 존재하는데, basis function의 수가 31을 넘는 것이다. 이 경우, regression approach 에 접근하면 데이터에 오버핏되기 쉽다. 그래서 일종의 페널티 값을 줌으로써 과적합을 막는 방법이 소개됐다. 거기서, 이 어프로치는 몇개의 파라미터를 더 요구한다. [Roughness penalty 선택] 함수의 roughness에 대한 척도로서 이차미분의 제곱[D2x(t)]2라고 정의하고, 이를 t에서의 curvature(곡률)라고 부른다. curvature가 없다는 말은 이계도함수가 0이라는 말과 같다. 그러면, 한 함수의 roughness 측도는 하식(2)과 같이 curvature의 적분값으로 정의된다. $PEN_2\left(x\right)\ =\ \int _{\ }^{\ }\left[D^2x\left(t\right)\right]^2\ dt\ \ \ \ \ \left(2\right)$PEN2(x) = ∫ [D2x(t)]2 dt (2) 단, 이러한 regression approach는 basis function의 수(여기서는 12)가 sampling points보다 훨씬 작은 경우에만 적합할 수 있다는 제약조건이 있다. 베이시스 기능 수가 크면 데이터를 과소평가하거나 과대평가할 가능성이 커지기 때문이다. 또, regression splines의 미분 추정치는 다소 불안정한 경향이 있다. 이에 smoothing의 제약조건이 조금 완화된 형태로 미분 추정치도 보다 정확하게 만들어내는 접근법이 연구됐다. [Data Smoothing with Roughness Penalties] roughness penalty 어프로치는 basis function의 수를 대폭 늘리는 것이다. 예를 들면, 상기의 growth 데이터는 아이 1명당 31개의 관측치가 존재하는데, basis function의 수가 31을 넘는 것이다. 이 경우, regression approach 에 접근하면 데이터에 오버핏되기 쉽다. 그래서 일종의 페널티 값을 줌으로써 과적합을 막는 방법이 소개됐다. 거기서, 이 어프로치는 몇개의 파라미터를 더 요구한다. [Roughness penalty 선택] 함수의 roughness에 대한 척도로서 이차미분의 제곱[D2x(t)]2라고 정의하고, 이를 t에서의 curvature(곡률)라고 부른다. curvature가 없다는 말은 이계도함수가 0이라는 말과 같다. 그러면, 한 함수의 roughness 측도는 하식(2)과 같이 curvature의 적분값으로 정의된다. $PEN_2\left(x\right)\ =\ \int _{\ }^{\ }\left[D^2x\left(t\right)\right]^2\ dt\ \ \ \ \ \left(2\right)$PEN2(x) = ∫ [D2x(t)]2 dt (2)

함수가 변수의 성격을 가지고 있으면 있을수록 curvature는 커지기 때문에 penaltyterm PEN2(x) 는 smoothing을 제공한다고 생각된다. 이를 응용하면 만약 이계 도함수의 형태에 관심이 있다면 PEN4(x)를 이용하면 된다. 그러나 roughness를 2번 미분과 연관시켜 보는 것이 아니라 어떤 함수가 smooth하는 것에서 먼 정도라고 보는 견해도 있다. 예를 들어 평균기온과 같이 기간에 영향을 받는 함수가 있다고 생각해 보자. 그러면, baseline의 움직임은 식 (3)과 같은 사인 곡선과 코사인 곡선의 변동으로 표현할 수 있다. $x\left(t\right)\ =\ c_0\ +\ a_1\sin \left(wt\right)\ +\ b_1\cos \left(wt\right)\ \ \ \ \ \left(3\right)$x(t) = c0 + a1sin(wt) + b1cos(wt) (3) 함수가 변수의 성격을 가지고 있을수록 curvature는 커지기 때문에 penaltyterm PEN2(x) 는 smoothing을 제공한다고 생각된다. 이를 응용하면 만약 이계 도함수의 형태에 관심이 있다면 PEN4(x)를 이용하면 된다. 그러나 roughness를 2번 미분과 연관시켜 보는 것이 아니라 어떤 함수가 smooth하는 것에서 먼 정도라고 보는 견해도 있다. 예를 들어 평균기온과 같이 기간에 영향을 받는 함수가 있다고 생각해 보자. 그러면, baseline의 움직임은 식 (3)과 같은 사인 곡선과 코사인 곡선의 변동으로 표현할 수 있다. $x\left(t\right)\ =\ c_0\ +\ a_1\sin \left(wt\right)\ +\ b_1\cos \left(wt\right)\ \ \ \ \ \left(3\right)$x(t) = c0 + a1sin(wt) + b1cos(wt) (3)

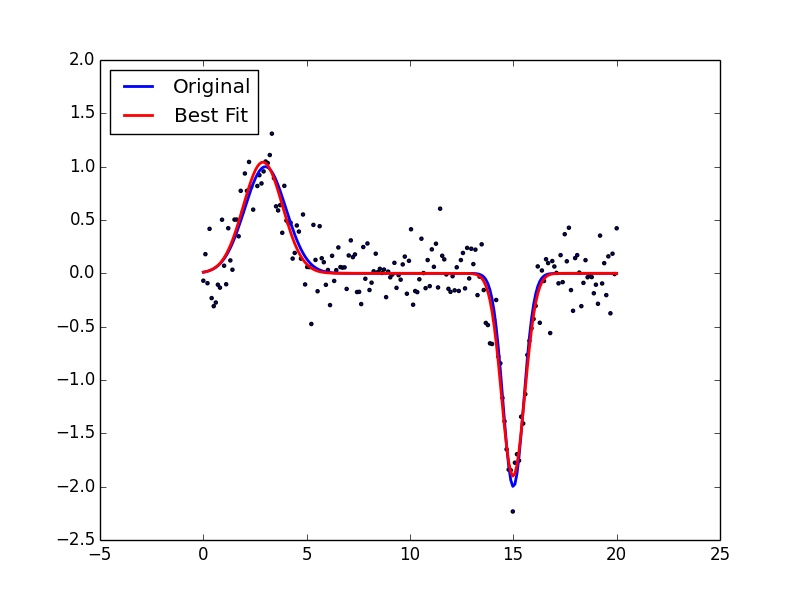
식(3)은 전 기간 T에 대해 w=2 π/T에 대해 Fourier의 전개가 가능하며, 이들 함수의 w2Dx+D3x를 계산하면 결과가 0임을 알 수 있다. 그리고 이때 L=w2D+D3를 harmonic acceleration operator라고 부르기로 했다. 이제 Fourier series인 정수 j에 대하여 operator를 적용하면 식(4) 와 같은 결과를 얻을 수 있다. $L\left(a_j\sin \left(jwt\right)\ +\ b_j\cos \left(jwt\right)\right)\ =\ w^2j\left(1-j^2\right)\left(a_j\cos \left(jwt\right)-b_j\sin \left(jwt\right)\right)\ \ \ \ \ \left(4\right)$L(ajsin(jwt) + bjcos(jwt)) = w2j(1-j2)(ajcos(jwt)-bjsin(jwt)) (4) 식 (3)은 전 기간 T에 대해 w=2 π/T에 대해 Fourier의 전개가 가능하며, 이들 함수의 w2Dx+D3x를 계산하면 결과가 0임을 알 수 있다. 그리고 이때 L=w2D+D3를 harmonic acceleration operator라고 부르기로 했다. 이제 Fourier series인 정수 j에 대하여 operator를 적용하면 식(4) 와 같은 결과를 얻을 수 있다. $L\left(a_j\sin \left(jwt\right)\ +\ b_j\cos \left(jwt\right)\right)\ =\ w^2j\left(1-j^2\right)\left(a_j\cos \left(jwt\right)-b_j\sin \left(jwt\right)\right)\ \ \ \ \ \left(4\right)$L(ajsin(jwt) + bjcos(jwt)) = w2j(1−j2)(ajcos(jwt)−bjsin(jwt)) (4)

식 (4)에서 j=1의 경우, L은 0이 되고, j의 숫자에 의해 L의 증가/감소가 결정되는 것을 알 수 있다. 이 불안정성을 제곱에 의해 극복하고 Penalty 성격을 부여하기 위해 위의 curvature 경우와 마찬가지로 Penalty 함수를 식(5)과 같이 정의할 수 있다. $PEN_L\left(x\right)\ =\ \int _{\ }^{\ }\left(Lx\left(s\right)\right)^2\ ds\ \ \ \ \ \left(5\right)$PENL(x) = ∫ (Lx(s))2 ds (5) 식 (4)에서 j=1의 경우, L은 0이 되고, j의 숫자에 의해 L의 증가/감소가 결정되는 것을 알 수 있다. 이 불안정성을 제곱에 의해 극복하고 Penalty 성격을 부여하기 위해 위의 curvature 경우와 마찬가지로 Penalty 함수를 식(5)과 같이 정의할 수 있다. $PEN_L\left(x\right)\ =\ \int _{\ }^{\ }\left(Lx\left(s\right)\right)^2\ ds\ \ \ \ \ \left(5\right)$PENL(x) = ∫ (Lx(s))2 ds (5)

Fourier series를 유한한 개수만큼 사용한다면, 식(5)은 j2(1-j2)2와 비례하게 된다. 또한 j=1의 경우 어떠한 penalty도 존재하지 않게 되며 order가 높은 항일일수록 더 높은 penalty 값을 부여받게 된다. 마지막으로 어떤 roughness 척도를 선택하더라도 사용할 때는 error sum of squares와 함께 혼합하여 사용하는데, 예를 들어 PEN2(x) 척도를 사용한다고 가정해 보자. 그러면 smoothing parameter λ을 설정하고, 하식(6)과 같이 최종적인 penalty 함수를 얻을 수 있다. $F\left(c\right)\ =\ \sum _{\ j}^{\ }\left[y_j\ -\ x\left(t_j\right)\right]^2\ +\ \lambda \int _{\ }^{\ }\left[D^2x\left(t\right)\right]^2\ dt\ \ \ \ \ \left(6\right)$F(c) = ∑ j[yj − x(tj)]2 + λ∫ [D2x(t)]2 dt (6) Fourier series를 유한한 개수만큼 사용한다면, 식 (5)은 j2(1-j2)2와 비례하게 된다. 또한 j=1의 경우 어떠한 penalty도 존재하지 않게 되며 order가 높은 항일일수록 더 높은 penalty 값을 부여받게 된다. 마지막으로 어떤 roughness 척도를 선택하더라도 사용할 때는 error sum of squares와 함께 혼합하여 사용하는데, 예를 들어 PEN2(x) 척도를 사용한다고 가정해 보자. 그러면 smoothing parameter λ을 설정하고, 하식(6)과 같이 최종적인 penalty 함수를 얻을 수 있다. $F\left(c\right)\ =\ \sum _{\ j}^{\ }\left[y_j\ -\ x\left(t_j\right)\right]^2\ +\ \lambda \int _{\ }^{\ }\left[D^2x\left(t\right)\right]^2\ dt\ \ \ \ \ \left(6\right)$F(c) = ∑ j[yj − x(tj)]2 + λ∫ [D2x(t)]2 dt (6)

여기서 λ는 첫 번째 term인 sum of squared residuals의 goodness-of-fit에 기초하여 penaltyterm인 curvature를 얼마나 강조할지를 결정하는 파라미터이다. 만약 λ 가 0에 가깝게 수렴한다면, penaltyterm인 curvature는 상대적으로 점차 커질 수 있다. 만약 λ가 너무 크면 penalty는 상대적으로 작아져야 하므로 curvature가 작아질 것이다. 따라서 λ가 0에 가까울수록 작다는 것은 함수 x가 제약 없이 basis function을 선택하여 자유롭게 데이터에 fit할 수 있다는 점을 의미한다. 종종 λ 를 로그 스케일로 변환하는 것이 편할 때도 있다. roughness를 정의하기 위해 differential operator L을 사용하면 λ가 무한대로 커질수록 데이터의 fit가 방정식 Lx = 0의 해에 접근하게 될 것이다. harmonic acceleration operator의 경우, 이해는 식(3)의 형태를 갖게 될 것이다. 이러한 방식으로 주로 사용하고자 하는 상황에 적절한 방식으로 smoothing process의 새로운 형태를 얻을 수 있다. [The Roughness Penalty Matrix R] 식(6)을 좀 더 일반화하면 식(7)과 같이 만들 수 있다. $F\left(c\right)\ =\ \sum _{\ j}^{\ }\left[y_j\ -\ x\left(t_j\right)\right]^2\ +\ \lambda \int _{\ }^{\ }\left[Lx\left(t\right)\right]^2dt\ \ \ \ \ \left(7\right)$F(c) = ∑ j[yj − x(tj)]2 + λ∫ [Lx(t)]2dt (7) 여기서 λ는 첫 번째 term인 sum of squared residuals의 goodness-of-fit에 기초하여 penaltyterm인 curvature를 얼마나 강조할지를 결정하는 파라미터이다. 만약 λ 가 0에 가깝게 수렴한다면, penaltyterm인 curvature는 상대적으로 점차 커질 수 있다. 만약 λ가 너무 크면 penalty는 상대적으로 작아져야 하므로 curvature가 작아질 것이다. 따라서 λ가 0에 가까울수록 작다는 것은 함수 x가 제약 없이 basis function을 선택하여 자유롭게 데이터에 fit할 수 있다는 점을 의미한다. 종종 λ 를 로그 스케일로 변환하는 것이 편할 때도 있다. roughness를 정의하기 위해 differential operator L을 사용하면 λ가 무한대로 커질수록 데이터의 fit가 방정식 Lx = 0의 해에 접근하게 될 것이다. harmonic acceleration operator의 경우, 이해는 식(3)의 형태를 갖게 될 것이다. 이러한 방식으로 주로 사용하고자 하는 상황에 적절한 방식으로 smoothing process의 새로운 형태를 얻을 수 있다. [The Roughness Penalty Matrix R] 식(6)을 좀 더 일반화하면 식(7)과 같이 만들 수 있다. $F\left(c\right)\ =\ \sum _{\ j}^{\ }\left[y_j\ -\ x\left(t_j\right)\right]^2\ +\ \lambda \int _{\ }^{\ }\left[Lx\left(t\right)\right]^2dt\ \ \ \ \ \left(7\right)$F(c) = ∑ j[yj − x(tj)]2 + λ∫ [Lx(t)]2dt (7)

 

order <- 6nbasis <- length(age) + order – 2 height basis <- create.bspline.basis(c(1,18), nbasis, order, age) heightfdPar <- fdPar (height basis, 4, 0.01) heightfd <- smooth.basis(age, growth$hgtm, heightfdPar)$plot(heightfd) order <- 6nbasis <- length(age) + order – 2 height basis <- create.bspline.basis(c(1,18), nbasis, order, age) heightfdPar <- fdPar (height basis, 4, 0.01) heightfd <- smooth.basis(age, growth$hgtm, heightfdPar)$plot(heightfd)

 

상기 예에서는 basisobejct(height basis), orderm(6), smoothing parameter(0.01)를 모두 알고 있으므로, fdPar()함수를 이용하여 fdPar 클래스 변환 후의 smooth.basis()함수를 이용하여 데이터를 Smooth하도록 하였다. 마지막으로 그 중에서 functional data ojbect(fd 클래스)만을 골라내어 함수로 그려보았다. [Choosing Smoothing Parameter λ] 지금부터 앞서 말한 문제를 해결해 보자. 적절한 λ값을 어떻게 찾을까? 여기에서는, 일반화 교차 검증(Generalized Cross Validationo; GCV)을 사용한다. 즉, 내가 생각할 때 적절해 보이는 λ 구간을 설정하고 그 구간 내 λ 값을 복수 검사한 후에 가장 적당한 값을 선택하는 방식이다. 여기서 GCV 척도를 하나 정하게 된다. 이는 위에서 구한 df(λ)를 활용하여 식(8) 와 같이 정의되는데, 우측 항에서 2 첫 번째 term은 regression analysis로 MSE의 오류 추정치와 비슷하다(n개 중에서 df(λ) 개를 추출한 것과 비슷하다). 이 GCV 척도를 이용해 최적의 λ값을 결정하도록 하자. $GCV\left(\lambda \right)\ =\ \left(\frac{n}{n-df\left(\lambda \right)}\right)\left(\frac{SSE}{n\ -\ df\left(\lambda \right)}\right)\ \ \ \ \ \left(8\right)$GCV(λ) = (nn−df(λ))(SSEn − df(λ)) (8) 상기 예에서는 basisobejct(height basis), orderm(6), smoothing parameter(0.01)를 모두 알고 있으므로, fdPar()함수를 이용하여 fdPar 클래스 변환 후의 smooth.basis()함수를 이용하여 데이터를 Smooth하도록 하였다. 마지막으로 그 중에서 functional data ojbect(fd 클래스)만을 골라내어 함수로 그려보았다. [Choosing Smoothing Parameter λ] 지금부터 앞서 말한 문제를 해결해 보자. 적절한 λ값을 어떻게 찾을까? 여기에서는, 일반화 교차 검증(Generalized Cross Validationo; GCV)을 사용한다. 즉, 내가 생각할 때 적절해 보이는 λ 구간을 설정하고 그 구간 내 λ 값을 복수 검사한 후에 가장 적당한 값을 선택하는 방식이다. 여기서 GCV 척도를 하나 정하게 된다. 이는 위에서 구한 df(λ)를 활용하여 식(8) 와 같이 정의되는데, 우측 항에서 2 첫 번째 term은 regression analysis로 MSE의 오류 추정치와 비슷하다(n개 중에서 df(λ) 개를 추출한 것과 비슷하다). 이 GCV 척도를 이용해 최적의 λ값을 결정하도록 하자. $GCV\left(\lambda \right)\ =\ \left(\frac{n}{n-df\left(\lambda \right)}\right)\left(\frac{SSE}{n\ -\ df\left(\lambda \right)}\right)\ \ \ \ \ \left(8\right)$GCV(λ) = (nn−df(λ))(SSEn − df(λ)) (8)

예를 들면, Canadian Weather 데이터 세트의 강수량 데이터를 보자. 예를 들면, Canadian Weather 데이터 세트의 강수량 데이터를 보자.

 

 

 

lambda <-1e6fdParobj <-fdPar(daybasis, harmaccelLfd, lambda) logprec です。fit <- smooth.basis(day.5, logprecav, fdParobj)logprec.fd <- logprec.fit$fdnames <-list(“Day (7月1日~6月30日)”, “ウェザーステーション” = カナダ語ですweather$place “ログ 10 降水量 (mm)” logprec.fd$fdnames <- fdnamesplot(logprec.fd, lty=1) です lambda <-1e6fdParobj <-fdPar(daybasis, harmaccelLfd, lambda) logprec です。fit <- smooth.basis(day.5, logprecav, fdParobj)logprec.fd <- logprec.fit$fdnames <-list(“Day (7月1日~6月30日)”, “ウェザーステーション” = カナダ語ですweather$place “ログ 10 降水量 (mm)” logprec.fd$fdnames <- fdnamesplot(logprec.fd, lty=1) です

 

이로써 최적의 lambda 값이 10의 6제곱임을 알 수 있었다. 그래서 이 lambda 값을 사용하여 위에서 진행한 과정과 동일하게 fd Par 클래스 변환한 후 smoothing하여 fd 클래스만 꺼내 플롯하였다. 그 결과는 위의 그래프와 같았다. 이로써 최적의 lambda 값이 10의 6제곱임을 알 수 있었다. 그래서 이 lambda 값을 사용하여 위에서 진행한 과정과 동일하게 fd Par 클래스 변환한 후 smoothing하여 fd 클래스만 꺼내 플롯하였다. 그 결과는 위의 그래프와 같았다.

protfit.fd(logprecav, day.5, logprec.fd) protfit.fd(logprecav, day.5, logprec.fd)

 

plotfit.fd(data) 함수를 사용하면 위와 같이 지정된 fdnames에 의해 각각 하나씩의 그래프를 따로 볼 수도 있다. [Constrained Function] 간혹 데이터가 하나 이상의 제약 조건을 충족해야 하는 경우가 있다. 예를 들어 카운트에 관한 함수는 값이 반드시 음수가 되는 것은 아니다. 누적되는 함수라면 곡선의 기울기가 음수가 될 수 없다. 그러나 이러한 basis function의 선형결합은 이러한 제약조건을 따로 고려하기 어렵다. 이에 대한 해법으로 추정하는 데이터 곡선 자체가 아무런 제약조건이 없는 상태로 바꾸려고 한다. 具体的には、positive smoothing、monotone smoothing、probability density function 方法がある. [Positive Smoothing] 먼저, 항상 positive 또는 negative의 경우를 살펴보자. 식(1)에서 x(t)=exp(w(t))로 바꾸면, w(t)는 부호에 제약을 받지 않는 함수가 된다. 동시에 피팅되는 함수는 항상 positive 값을 갖게 된다. w(t) 값이 매우 작은 값이 되면 x(t) 는 0에 가까워지다. 예를 들어 밴쿠버의 하루 평균 강수량 데이터를 Smooth 시켜보자. 이 데이터는 0의 값을 가질 수는 있지만 음의 값을 가질 수는 없다. plotfit.fd(data) 함수를 사용하면 위와 같이 지정된 fdnames에 의해 각각 하나씩의 그래프를 따로 볼 수도 있다. [Constrained Function] 간혹 데이터가 하나 이상의 제약 조건을 충족해야 하는 경우가 있다. 예를 들어 카운트에 관한 함수는 값이 반드시 음수가 되는 것은 아니다. 누적되는 함수라면 곡선의 기울기가 음수가 될 수 없다. 그러나 이러한 basis function의 선형결합은 이러한 제약조건을 따로 고려하기 어렵다. 이에 대한 해법으로 추정하는 데이터 곡선 자체가 아무런 제약조건이 없는 상태로 바꾸려고 한다. 具体的には、positive smoothing、monotone smoothing、probability density function 方法がある. [Positive Smoothing] 먼저, 항상 positive 또는 negative의 경우를 살펴보자. 식(1)에서 x(t)=exp(w(t))로 바꾸면, w(t)는 부호에 제약을 받지 않는 함수가 된다. 동시에 피팅되는 함수는 항상 positive 값을 갖게 된다. w(t) 값이 매우 작은 값이 되면 x(t) 는 0에 가까워지다. 예를 들어 밴쿠버의 하루 평균 강수량 데이터를 Smooth 시켜보자. 이 데이터는 0의 값을 가질 수는 있지만 음의 값을 가질 수는 없다.

lambda <- 1e3WfdParobc <- fdPar (daybasis, harmaccelLfd, lambda) vanPrec <- カナダ語です天気$dailyですAv[dayOfYearShifted, ‘Vancouver’, ‘Precipitation.mm ‘] VanPrecPos <- smooth.pos (day.5, vanPrec, WfdParobc)Wfd <- VanPrecPos$WfdobjWfd$fdnames <-list(“Day(7月1日~6月30日)”, “Weather Station” = カナダ語ですweather$place”Log 10 Critation (mm)” precfit <-exp(eval.fd(day.5, wfd))plot(day.5, vanPrec, type=’p’, cex=1.2, xlab=”Day(7月1日から6月30日)”, ylab=”ミリメートル”, main = “バンクーバーの降水量”)行(day.5, precfit、lwd=2) lambda <- 1e3WfdParobc <- fdPar (daybasis, harmaccelLfd, lambda) vanPrec <- カナダ語です天気$dailyですAv[dayOfYearShifted, ‘Vancouver’, ‘Precipitation.mm ‘] VanPrecPos <- smooth.pos (day.5, vanPrec, WfdParobc)Wfd <- VanPrecPos$WfdobjWfd$fdnames <-list(“Day(7月1日~6月30日)”, “Weather Station” = カナダ語ですweather$place”Log 10 Critation (mm)” precfit <-exp(eval.fd(day.5, wfd))plot(day.5, vanPrec, type=’p’, cex=1.2, xlab=”Day(7月1日から6月30日)”, ylab=”ミリメートル”, main = “バンクーバーの降水量”)行(day.5, precfit、lwd=2)

 

positive 값만을 갖는 functional data objects를 Smooth하는 데에는 Smooth.pos() 함수를 이용했다. 그 중에서 fd 클래스를 뽑아 Wfd로 저장하고 evaluate한 결과를 지수 변환하여 플롯한 그래프는 위와 같다. [Monotone Smoothing] 관측치가 완벽한 monotone 성질을 나타내지 않아도 fitting된 함수 x(t) 그럼 monotone한 함수가 필요한 경우가 있다. 우선, 식 (9)과 같은 함수 형태를 가정해 보자. $y_j\ =\ \beta _0\ +\ \beta _1x\left(t_j\right)\ +\ \epsilon _j\ \ \ \ \ \left(9\right)$yj = β0 + β1x(tj) + εj(9) positive 값만을 갖는 functional data objects를 Smooth하는 데에는 Smooth.pos() 함수를 이용했다. 그 중에서 fd 클래스를 뽑아 Wfd로 저장하고 evaluate한 결과를 지수 변환하여 플롯한 그래프는 위와 같다. [Monotone Smoothing] 관측치가 완벽한 monotone 성질을 나타내지 않아도 fitting된 함수 x(t) 그럼 monotone한 함수가 필요한 경우가 있다. 우선, 식 (9)과 같은 함수 형태를 가정해 보자. $y_j\ =\ \beta _0\ +\ \beta _1x\left(t_j\right)\ +\ \epsilon _j\ \ \ \ \ \left(9\right)$yj = β0 + β1x(tj) + εj (9)

이번에는 식 (1)에서 x(t)=∫exp[w(u)]du, (t0<u<t)로 바꿔 보자. t0은 t값의 범위 중에서 시작점이며, intercept term인 β0는 시작점 t0에서 함수의 근사치로 추정된다. 이를 식(9)에 대입하면 식(10)과 같음을 알 수 있다. $y_j\ =\ \beta _0\ +\ \beta _1\int _{t_0}^{t_j}\exp \left[w\left(u\right)\right] du\ +\ \epsilon _j\ =\ \beta _0\ +\ \beta _1\int _{t_0}^{t_j}\exp \left[\Phi \left(u\right)”c\right] du\ +\ \epsilon _j\ \ \ \ \ \left(10\right)$yj = β0 + β1∫tjt0exp[w(u)] du + εj = β0 + β1∫tjt0exp[Φ(u)′c] du + εj(10) 이번에는 식 (1)에서 x(t)=∫exp[w(u)]du, (t0<u<t)로 바꿔 보자. t0은 t값의 범위 중에서 시작점이며, intercept term인 β0는 시작점 t0에서 함수의 근사치로 추정된다. 이를 식(9)에 대입하면 식(10)과 같음을 알 수 있다. $y_j\ =\ \beta _0\ +\ \beta _1\int _{t_0}^{t_j}\exp \left[w\left(u\right)\right] du\ +\ \epsilon _j\ =\ \beta _0\ +\ \beta _1\int _{t_0}^{t_j}\exp \left[\Phi \left(u\right)”c\right] du\ +\ \epsilon _j\ \ \ \ \ \left(10\right)$yj = β0 + β1∫tjt0exp[w(u)] du + εj = β0 + β1∫tjt0exp[Φ(u)′c] du + εj (10)

상기 positive의 경우에 smooth.pos() 함수를 사용한 것처럼, 이 경우에는 smooth.monotone() 함수를 사용하면 된다. 상기 positive의 경우에 smooth.pos() 함수를 사용한 것처럼, 이 경우에는 smooth.monotone() 함수를 사용하면 된다.

 

 

(MFho)wo-c)가 크뤼스-carcarcatsthatsthis = (c)가)비명자낮은 (c, 35, 35, 6)의 그로페 <UNT_PHL> (c)의)의 밑바닥에 의해 10, 10, 10 (c)의 밑바닥에 의해, 10, 105))그로몬트몽디스제노네(Grgwdp) で す す でWefo-dpwhhhhhpo) 、 w す d – w

 

[Probability Density Functions] 있는 PDF p(x) 는 positive function의 한 케이스라고 생각된다. 그렇다면 어떤 z에 대해 식(11)의 비율로 나타낼 수 있다. 여기서 C는 p(z)의 integral이 1이 되도록(확률함수가 될 필요가 있기 때문에) 만들어 주는 normalizing constant라고 생각하자. $p\left(z\right)\=\cdot \exp\left[w\left(z)\right] @ \ \ \ le $(z)= C·exp[w(z)](11) [Probability Density Functions] 있는 PDF p(x) 는 positive function의 한 케이스라고 생각된다. 그렇다면 어떤 z에 대해 식(11)의 비율로 나타낼 수 있다. 여기서 C는 p(z)의 integral이 1이 되도록(확률함수가 될 필요가 있기 때문에) 만들어 주는 normalizing constant라고 생각하자. $p\left(z\right)\=\cdot \exp\left[w\left(z)\right] @ \ \ \ le $(z)= C·exp[w(z)](11)

non-parametric한 버전을 추정하는 것은 smoothing과는 연관이 없기 때문에 여기서는 penalized negative log likelihood를 최소화하는 방법을 알아보자。 $-\ln \left(L\left(c\right)\right)\ =\ -\sum _i^N\ln \ p\left(z_i\right)\ +\ \lambda \int _{\ }^{\ }\left[Lw\left(z\right)\right]^2dz\ =\ -\sum _i^Nw\left(z_i\right)\ -\ N\ln C\ +\ \ \lambda \int _{\ }^{\ }\left[Lw\left(z\right)\right]^2dz\ \ \ \ \ \left(12\right)$−ln(L(c)) = −N∑iln p(zi) + λ∫ [Lw(z)]2dz = −N∑iw(zi) − NlnC + λ∫ [Lw(z)]2dz (12) non-parametric한 버전을 추정하는 것은 smoothing과는 연관이 없기 때문에 여기서는 penalized negative log likelihood를 최소화하는 방법을 알아보자。 $-\ln \left(L\left(c\right)\right)\ =\ -\sum _i^N\ln \ p\left(z_i\right)\ +\ \lambda \int _{\ }^{\ }\left[Lw\left(z\right)\right]^2dz\ =\ -\sum _i^Nw\left(z_i\right)\ -\ N\ln C\ +\ \ \lambda \int _{\ }^{\ }\left[Lw\left(z\right)\right]^2dz\ \ \ \ \ \left(12\right)$−ln(L(c)) = −N∑iln p(zi) + λ∫ [Lw(z)]2dz = −N∑iw(zi) − NlnC + λ∫ [Lw(z)]2dz (12)

여기서, w(z) = c’* Φ(z) 이며, 앞의 2개 항은 error sum of squares라고 생각하면 된다. 여기서 Linear differential operator인 L은 λ가 무한대로 발산함에 따라 어떤 parametric한 PDF로 근사하도록 설정한다. 예를 들면, L = D3의 경우에는 가우스 함수로 수렴한다. [Assesing the Fit to the Data] 데이터를 smooth하도록 만들었다면 잔차(residuals)를 이용해 내가 만든 모형이 얼마나 잘 fit됐는지 검정하는 과정이 필요하다. 이때 i번째 객체인 j 첫 번째 변수에 대한 잔차 rij = yij – xi(tj)로 정의된다. 즉, 실제 y와 fitted value의 차이 값이다. 여기서, w(z) = c’* Φ(z) 이며, 앞의 2개 항은 error sum of squares라고 생각하면 된다. 여기서 Linear differential operator인 L은 λ가 무한대로 발산함에 따라 어떤 parametric한 PDF로 근사하도록 설정한다. 예를 들면, L = D3의 경우에는 가우스 함수로 수렴한다. [Assesing the Fit to the Data] 데이터를 smooth하도록 만들었다면 잔차(residuals)를 이용해 내가 만든 모형이 얼마나 잘 fit됐는지 검정하는 과정이 필요하다. 이때 i번째 객체인 j 첫 번째 변수에 대한 잔차 rij = yij – xi(tj)로 정의된다. 즉, 실제 y와 fitted value의 차이 값이다.

par(mfrow=c(1,1))logprecmat <- eval.fd(day.5, logprec.fd)logprecres <- logprecav – logprecmatlogprecvar1 <- apply(logpres^2, 1, sum)/35log precvar2 <- apply(loge^2, 2, sum)/(365-12)logedeval.basis(day.fd)logevarobj$fd)fd、 ylab=’日をまたいでの標準偏差’, pch=19)text(1:35, logprecvar2+0.001, colnames(logprecres)) par(mfrow=c(1,1))logprecmat <- eval.fd(day.5, logprec.fd)logprecres <- logprecav – logprecmatlogprecvar1 <- apply(logpres^2, 1, sum)/35log precvar2 <- apply(loge^2, 2, sum)/(365-12)logedeval.basis(day.fd)logevarobj$fd)fd、 ylab=’日をまたいでの標準偏差’, pch=19)text(1:35, logprecvar2+0.001, colnames(logprecres))

 

GCV를 적용하여 최적의 lambda를 찾고 이를 fd Par 클래스로 변환한 후 smooth.basis() 함수로 basis function을 smooth 시킨 추정치의 fd 클래스를 logprec.fd로 저장했다는 점을 기억하자. 이것을 evaluate 하면, 35*365의 fitted value 행렬을 얻을 수 있다. 이 행렬과 실제 값과의 차이를 잔차로 하여 잔차 행렬을 logprecres에 저장하였다. 그 후, 잔차 행렬을 행에 대해, 열에 대해 각각 잔차 제곱합을 구한 후, n으로 나누어 standard deviation을 구하면, 날짜에 따라, 관측소에 따라 잔차 검정을 하기 위한 준비가 끝난다. (여기서 12를 뽑는 이유는 degree of freedom을 맞추기 위해서다) 이것을 그래프로 나타내면 위와 같다. station number가 커지면서 우상향하는 경향이 있지만 그렇게 극적인 차이를 만들어낼 것 같지는 않다. GCV를 적용하여 최적의 lambda를 찾고 이를 fd Par 클래스로 변환한 후 smooth.basis() 함수로 basis function을 smooth 시킨 추정치의 fd 클래스를 logprec.fd로 저장했다는 점을 기억하자. 이것을 evaluate 하면, 35*365의 fitted value 행렬을 얻을 수 있다. 이 행렬과 실제 값과의 차이를 잔차로 하여 잔차 행렬을 logprecres에 저장하였다. 그 후, 잔차 행렬을 행에 대해, 열에 대해 각각 잔차 제곱합을 구한 후, n으로 나누어 standard deviation을 구하면, 날짜에 따라, 관측소에 따라 잔차 검정을 하기 위한 준비가 끝난다. (여기서 12를 뽑는 이유는 degree of freedom을 맞추기 위해서다) 이것을 그래프로 나타내면 위와 같다. station number가 커지면서 우상향하는 경향이 있지만 그렇게 극적인 차이를 만들어낼 것 같지는 않다.

플롯(exp(log(log(logprecvar1))/2), pch=19, xlab=’Day’, ylab=’ステーション間の標準偏差’)行(day.5, logprecvar1fit, lwd=2, col=’blue’) 플롯(exp(log(log(log(logprecvar1)), pch=19, xlab=’Day’, ylab=’ステーション間の標準偏差’)行(day.5, logprecvar1fit, lwd=2, col=’blue’)

 

파란 선은 variance의 로그 변환을 smooth로 한 후 다시 지수 변환으로 되돌린 선이라고 생각하면 된다. 굳이 로그 변환을 한 이유는 강수량 데이터가 강하게 편중돼 있기 때문에(skewed) 로그 변환을 하면 효과적으로 location을 찾을 수 있기 때문이다. 파란 선은 variance의 로그 변환을 smooth로 한 후 다시 지수 변환으로 되돌린 선이라고 생각하면 된다. 굳이 로그 변환을 한 이유는 강수량 데이터가 강하게 편중돼 있기 때문에(skewed) 로그 변환을 하면 효과적으로 location을 찾을 수 있기 때문이다.